Какую часть часа составляют 4 минуты, какую часть часа составляет а)36 минут б)15 минут в) 3 минут

Предусмотрена подвеска под крылом, на внешних пилонах, двух сбрасываемых топливных баков емкостью по литров каждый [8]. Носовая часть фюзеляжа изготовлена из алюминиевых сплавов и включает отсек радиоэлектронного оборудования, кабину экипажа и закабинный отсек оборудования; спереди к носовой части пристыковывается радиопрозрачный обтекатель антенны радиолокационного прицела. Эвакуация жителей тысячного города была проведена быстро, утверждает Арутюнян.
Запиши в виде процентов Запиши какую часть метра составляет 1 2 9 см? Какую часть центнера составляет 1 кг 25 кг 87 кг? Ответ на вопрос. Математика - 3 года назад. Сколько здесь прямоугольников.
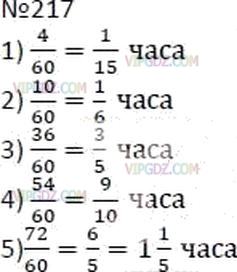
История - 4 года назад. Литература - 4 года назад. Русский язык - 4 года назад. Физика - 4 года назад. Информация Посетители, находящиеся в группе Гости , не могут оставлять комментарии к данной публикации. Сведения об использовании дробей в Древнем Египте восходят примерно к году д.
Этот древний документ показывает, что египтяне широко использовали дроби для решения повседневных проблем, от распределения продуктов питания и товаров до управления землей и ресурсами. Другие дроби выражались как суммы этих единичных дробей, демонстрируя сложный метод дробного представления. Переписанный писцом Ахмесом примерно в году до н. Каждая дробь с числителем, равным единице, изображалась путем размещения иероглифа "часть" символ рта над числом знаменателя.
Необходимость точного измерения и перераспределения земель после ежегодного разлива Нила подтолкнула египтян к использованию дробей как единиц измерения для решения практических задач.
Это демонстрирует не только их математическую изобретательность, но и важнейшую роль дробей в удовлетворении насущных потребностей древнеегипетской цивилизации. Вавилоняне древней Месопотамии, процветавшей примерно с по год до н. Центральное место в их математических достижениях занимала разработка шестидесятеричной системы счисления, подхода, который способствовал использованию дробей.
Вавилонские астрономы и математики создали сложную систему астрономии и хронометража, основанную на шестидесятеричной системе счисления. Это потребовало тонкого применения дробей, особенно для деления времени на более мелкие единицы. Именно их понимание учета времени позволило разделить часы на минуты и секунды, и эта концепция продолжает определять наше восприятие времени.
Глобальное наследие их системы наиболее очевидно в минутных часах и градусном круге, которые стали фундаментальными для того, как мы понимаем и измеряем время и пространство.
Такой подход обеспечивал достаточную простоту представления в математических и астрономических расчетах. Выбор вавилонянами шестидесятеричной системы счисления оказал глубокое влияние на математическую и научную сферы, продемонстрировав также умение работать с дробями.
В период около г. Эти древние тексты, необходимые для точного строительства алтарей и проведения религиозных церемоний, демонстрируют понимание дробей, которое близко отражает современную практику.
Шульба-сутры не только демонстрируют практическое применение дробей в религиозном и архитектурном контексте, но и отражают работу ранних индийских математиков со сложными математическими концепциями. Сутры Шульбы составляют важнейшую часть более широкой коллекции, известной как Шраута-сутры, которые сами по себе являются продолжениями Вед, классифицируемыми как веданги.
Эти тексты представляют собой единственный источник знаний по индийской математике ведической эпохи, в которых рассматриваются геометрические принципы и проблемы, связанные с прямолинейными фигурами, их комбинациями, преобразованиями и даже задачей возведения круга в квадрат.

Кроме того, они охватывают алгебраический и арифметический подходы к этим геометрическим дилеммам. Важно отметить, что составители сутр Шульбы продемонстрировали четкое понимание дробей, интегрировав эти знания в свои математические решения.
Более того, эти сутры сложным образом связывают дизайн алтарей для жертвенного огня с божественными атрибутами, предполагая, что уникальные конфигурации этих алтарей символизируют особые благословения, дарованные богами.
В Индии дроби известны с древнейших времен. Уже в середине 2 тысячелетия д. Записывались они без дробной черты, но также — числитель над знаменателем и отделялись друг от друга вертикальными и горизонтальными линиями. Математики Древней Индии не ограничивались базовыми операциями с дробями.
Вместо этого они углубились в более сложные теории рациональных чисел, проложив путь к распознаванию отрицательных дробей и концепции нуля. Уникальным аспектом древнеиндийской математики было использование звуковых символов для представления дробей. Эта инновационная система счисления позволила математикам передавать сложные математические идеи посредством устной традиции задолго до широкого использования письменных математических текстов.
Один из основополагающих китайских математических текстов "Девять глав о математическом искусстве" датируется примерно 1 веком д. Эта всеобъемлющая работа иллюстрирует не только мастерство китайцев в обращении с числами, но и их изощренный подход к работе с дробями. В тексте представлены методы нахождения общих знаменателей для сложения дробей, отражающие раннее и глубокое понимание дробной арифметики.
Использование дробей в древнекитайской математике не стояло изолированно, а было ключевым компонентом более широкой математической системы, которая решала различные практические и теоретические проблемы.
Задайте его нашему сообществу, у нас наверняка найдется ответ! Делитесь опытом и знаниями, зарабатывайте награды и репутацию, заводите новых интересных друзей! Задавайте интересные вопросы, давайте качественные ответы и зарабатывайте деньги.
Статистика проекта за месяц. Подтверждаю согласие с Политикой конфиденциальности. Светланочка [50K] 6 лет назад Математика.
Ответы к игре на 1- 8 фото?